Radiação Eletromagnética
A luz é uma radiação eletromagnética, ou seja, possui ao mesmo tempo os componentes elétrico e magnético enquanto se desloca através do espaço com velocidade c = 3,0.108 m/s.
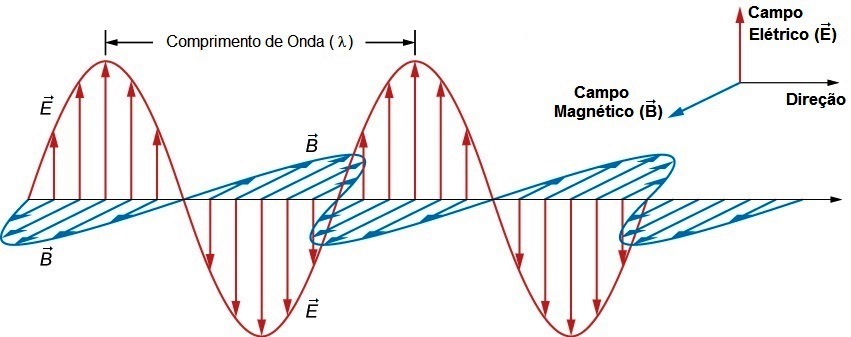
Pode ser descrita matematicamente por uma função de onda e possui as propriedades frequência (υ, s-1 = Hz) e comprimento de onda (λ, m) que determinam sua energia:
E = hυ; c = λυ ∴ E = hc/λ
onde h = constante de Planck.
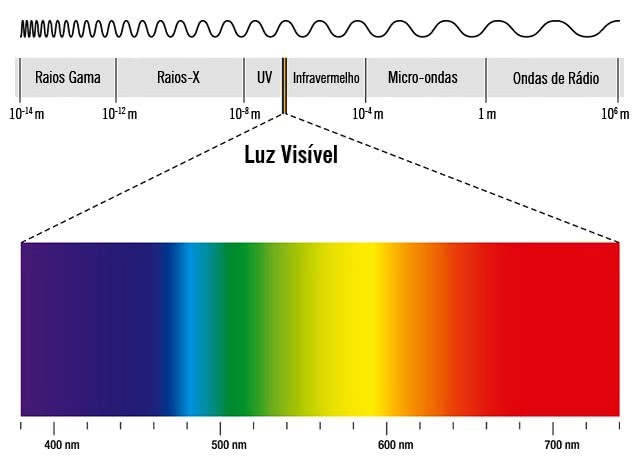
Assim, quanto maior a frequência e menor o comprimento de onda, maior a energia. O espectro eletromagnético classifica a radiação em função de seu comprimento de onda, desde baixas à altas energias. A radiação visível, por exemplo, se encontra entre 400-700 nm.
Introdução à Mecânica Quântica - Modelo Atômico de Bohr
Após defender seu doutorado, Niels Bohr foi à Inglaterra para se tornar aluno de Joseph Thomson, o descobridor do elétron em 1897. Lá conheceu, se tornou amigo e foi trabalhar com Ernest Rutherford, então ex-aluno de Thomson, que tinha feito importantes descobertas sobre o núcleo do átomo.
Rutherford formulou uma teoria simples baseada em um modelo planetário que estivesse de acordo com seus experimentos, mas Bohr notou muitas incoerências nesse modelo. Ao aperfeiçoar o modelo de Rutherford, Bohr percebeu que havia a necessidade de que os elétrons tivessem apenas energias discretas e que deveriam passar de um estado de energia para outro sem energias intermediárias. Esse fenômeno é chamado de quantização da energia e já tinha sido deduzido por Planck em seu estudo sobre radiações eletromagnéticas, que foi amplamente aproveitado por Bohr em seu modelo atômico em 1913.
Segundo Bohr, os elétrons estão arranjados em diferentes níveis de energia e percorrem órbitas em torno do núcleo. As energias em cada órbita possuem apenas valores múltiplos da constante ℏ (ℏ = h/2π) e a transição entre níveis ocorre através de fótons, onde um fóton é emitido ou absorvido pela exata diferença entre níveis da órbita do elétron. Seu modelo permitiu determinar, dentre outras coisas, o raio mínimo da órbita do elétron no hidrogênio e explicou satisfatoriamente o espectro de linhas do hidrogênio.
Camada |
Nível (n) |
Máx. de elétrons |
| K | 1 | 2 |
| L | 2 | 8 |
| M | 3 | 18 |
| N | 4 | 32 |
| O | 5 | 32 |
| P | 6 | 18 |
| Q | 7 | 2 |
Apesar de ter acumulado muitos sucessos respondendo a várias questões sobre a natureza do átomo, seu modelo também demonstrou algumas fragilidades:
- só é aplicável ao hidrogênio ou a átomos hidrogenóides (com apenas um elétron),
- o átomo de hidrogênio deveria ser um disco plano,
- ainda não explicava todas as linhas do espectro de linhas do hidrogênio,
- a noção de órbita definida para o elétron está em contradição com o Princípio de Incerteza de Heisenberg (1927) de que não é possível conhecer a energia e a posição do elétron simultaneamente de forma exata.
O modelo de Bohr foi um passo decisivo em direção à quantização da energia no átomo e em suas interações com a luz.
Introdução à Mecânica Quântica - Dualidade Onda-Partícula - Descrição Ondulatória do Elétron
A ideia de que o elétron fosse uma partícula encontrava grande suporte experimental até que, através da experiência da fenda dupla, foi possível observar a difração do elétron - um fenômeno típico de ondas.
Esse comportamento duplo de onda e partícula para a matéria tinha sido previsto poucos anos antes por Louis de Broglie através da relação:
λ = h/p
onde p = mv (momento)
Dessa forma, toda a matéria pode assumir comportamento de onda e de partícula. Para um carro, por exemplo, sua massa é relativamente tão grande que o comprimento de onda associado não pode ser observado experimentalmente. por outro lado, o elétron tem massa pequena o suficiente para que seu comprimento de onda possa ser detectado.
Essa relação ajudou a corroborar a mecânica quântica na descrição de sistemas microscópicos abrindo a possibilidade de que o elétron pudesse ser tratado matematicamente como uma função de onda (Ψ), permitindo assim uma nova abordagem dos átomos e de suas ligações químicas.
